아래 글은 모두 'step by step [파이썬 비즈니스 통계분석]' 교재를 기초로 진행한 내용입니다. 모든 장은 이전 장과 이어져 있으니, 세부 내용 및 이전 글이 궁금하시다면 해당 블로그의 이전 장들을 참고해주시면 되겠습니다.~~
1. 회귀분석이란?
하나 이상의 수치형 변수들을 독립변수(또는 예측변수)로, 또 다른 결과적인 수치형 변수를 종속변수(또는 반응변수)로 설정해, 개별 독립변수의 변화에 어떻게 영향을 미치는지 판단한다. 만약 독립변수들의 값이 주어졌을 때, 종속변수의 값을 예측하거나 독립변수와 종속변수 간의 인과관계를 검증할 수 있는 통계분석 기법이다. (가장 널리 알려진 기법 중 하나!!)
Ex) 광고의 횟수와 매출액의 관계, 구매유형에 따른 고객만족도의 관계.
회귀분석 모형은 독립변수 및 종속변수의 개수와 형태에 따라 다양한 모형으로 분류된다. 1) 독립변수와 종속변수가 각각 한 개씩이면서 모두 수치형 변수인 경우, 단순회귀모형이 된다. 2) 1개의 수치형 종속변수와 2개 이상의 독립변수가 있을 때는 다중회귀모형으로 불린다. 이 때 다중회귀모형의 독립변수는 수치형일 수도, 범주형일 수도 있다.
cf) 보통 수치형인 독립변수들을 대상으로 하지만, 범주형 변수를 더미변수(dummy variable)로 전환해 회귀모형에 포함시킴으로써 다중회귀모형의 활용성을 넓히기도 한다.
2. 회귀분석의 종류

회귀분석을 진행하기 위한 전제조건 4가지
선형성, 등분산성, 독립성, 정규성
- 독립변수와 종속변수 간에는 선형관계가 존재한다.
- 잔차들은 동일한 분산을 갖는다.
- 잔차들은 서로 독립이다.
- 잔차는 평균이 0이고 분산이 sigma ^2인 정규분포를 따른다.
해당 절에서는 독립변수의 수에 따른 단순회귀분석, 다중회귀분석 방법만을 다루었습니다!
1) 단순회귀분석
고객만족도와 실제 고객구매액 간의 연관성은 상관관계 분석을 통해서 검증이 가능하다. 그런데 고객만족도가 구매액에 영향을 미치는 것일까, 아니면 구매액 수준이 만족도에 영향을 미치는 것일까? (고객만족도가 기대수준과 실제 경험의 차이에서 오는 개념이기 때문에, 구매액이 높은 사람일수록 고객만족도가 높을 소지도 있다!) 이럴 때 우리는 단순회귀분석을 통해 의문을 해결할 수 있다. -> 1개의 수치형 독립변수(ex. 고객만족도)가 1개의 수치형 종속변수(ex. 고객 구매액)에 어떤 영향을 미치는지 검정하는 통계분석이기 때문!!
독립변수 X와 종속변수 Y를 갖는 단순회귀모형👇
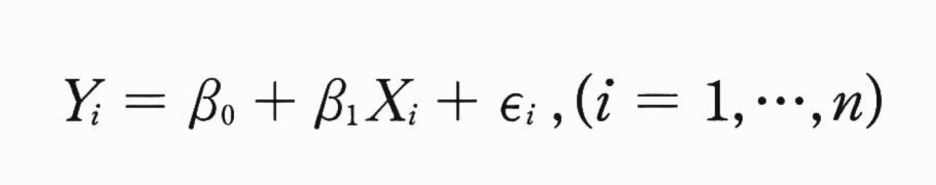
여기서 e(i, i = 1, 2, ...n)들은 잔차(오차)들로, 서로 독립이다. 평균은 0이며, 분산 sigma^2인 정규분포를 따르는 확률변수이다. n개의 주어진 데이터 (X1, Y1), (X2, Y2)... (Xn, Yn)으로부터 우리는 적절한 방법으로 B0, B1을 추정해야 한다. 그 추정치를 각각 b0, b1이라고 하면 우리는 다음과 같은 회귀직선👏을 구할 수 있다.

모형 도출 방법
최소제곱법
회귀 분석에서 회귀 모형 추정은 수집된 데이터를 바탕으로 가장 적절한 회귀 직선을 구하는 것이다. 이 방법 가운데 하나가 최소제곱법이다. 앞서 나온 회귀식의 b0와 b1의 값은 최소제곱법에 의해 구할 수 있는데, 오차제곱합을 최소로 하는 B0, B1값을 구한다.
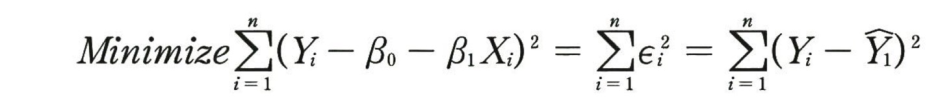
-> 최소제곱법에 의해 추정된 b0(절편)와 b1(기울기)는 다음과 같이 주어진다.

cf) b0의 값을 회귀식에 대입하면 추정된 회귀식은 항상 독립변수의 평균값과 종속변수의 평균값 (E[X], E[Y])를 지나면서 기울기가 b1인 직선이 됨을 알 수 있다.
설명력 지표
결정계수
회귀직선을 적합시킨 후 회귀선의 설명력을 나타내는 지표로 결정계수 R^2을 주로 사용한다. 종속변수의 총 제곱합 중에서 회귀직선에 의해 설명된 제곱합의 비율로, 항상 0과 1 사이의 값을 갖는다. 1에 가까울수록 적합된 회귀직선의 설명력이 높다고 할 수 있다. 단순회귀모형에서의 결정계수는 항상 독립변수와 종속변수 간의 상관계수의 제곱과 같다!
Ex) 두 변수 간의 상관계수가 0.9 또는 -0.9라고 했을 때, 결정계수는 0.81(or 81%)가 된다. 이 경우, 종속변수의 총 제곱합 중 약 81%가 적합된 회귀직선에 의해 설명된다고 해석한다.

회귀분석의 적합성 평가
회귀식의 통계적 유의성을 객관적으로 평가할 수 있는 방법에는 분산분석표를 활용하는 방법이 있다. 회귀선의 설명력이 높아도 통계적으로 유의하지 않으면 일반화해 사용하기 어렵다.
회귀분석을 분산분석의 관점에서 살펴보면, 주어진 독립변수에 따라 종속변수의 평균을 나타내는 회귀선과 집단 전체의 평균 차이를 실제 관측치가 회귀선으로부터 떨어져 있는 잔차와 비교해 통계적으로 유의하게 다른가 분석하는 것이 된다.
- 독립변수 -> 종속변수 평균 (회귀선 예측)
- 집단 전체 -> 평균 (실제 관측치)
실제 관측치 - 회귀선 = 잔차
이 잔차를 두고 우리는 회귀식의 통계적 유의성을 판단한다!!
회귀분석의 가정들은 모형 적합 후에 나타나는 잔차들을 통해 확인하게 된다. 즉, 주어진 데이터(Xi, Yi)에서 종속변수의 실제 값은 Yi이고, 독립변수 Xi의 값에서 추정된 종속변수의 값은 회귀식에 Xi를 대입함으로써 Yi = b0 + b1Xi로 구할 수 있다.
이때의 잔차들로 우리는 잔차그림을 통해 회귀모형의 가정들을 확인한다. 표준화된 잔차들을 r1, ...rn이라고 할 때, 종속변수 추정치와 잔차 간의 산점도 또는 독립변수와 잔차 간의 산점도를 통해 회귀모형들의 가정들을 체크한다. 그리고 잔차를 통한 회귀진단 결과 가정이 적합하지 않으면, 회귀모형을 수정한다!
# 실습
A쇼핑의 방문빈도와 총 매출액의 인과관계를 회귀분석을 통해 알아보자.
- H0 = 방문빈도는 총 매출액에 영향을 미치지 않는다.
- H1 = 방문빈도는 총 매출액에 영향을 미친다.
import statsmodel.formula.api as smf
model1 = smf.ols(formula = '총_매출액 ~ 방문빈도', data = df).fit()
model1.summary()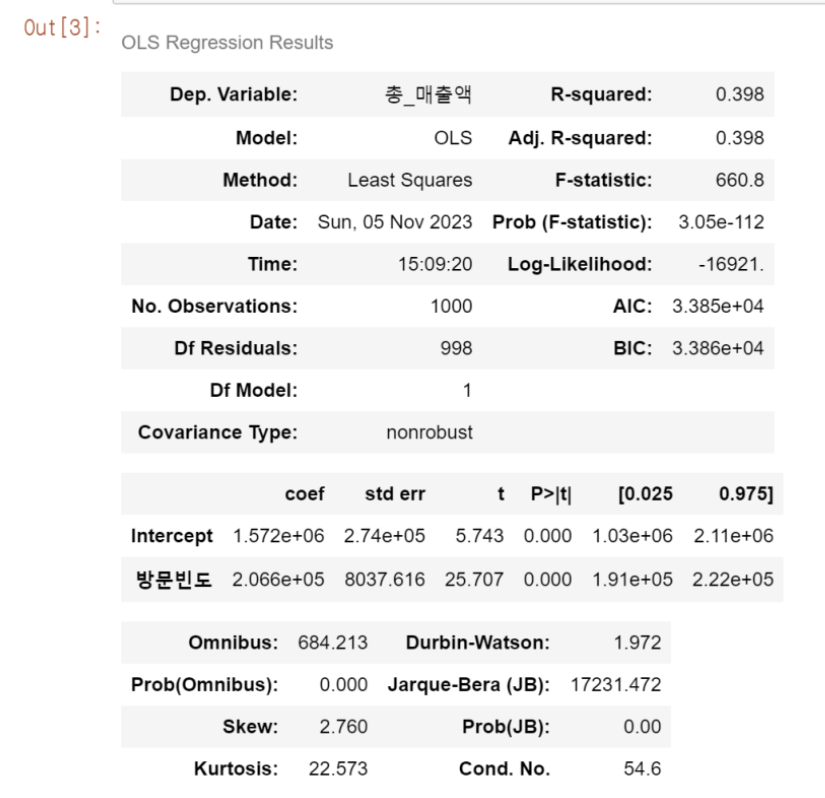
1. 첫 번째 테이블은 종속변수, 결정계수, 분석모델, 조정결정계수, model 계산방식 등이 출력된다. F-statistics는 회귀모형의 적합도를 나타내는 통계량이고, Prob(F-statistic)는 F검정 통계량의 유의확률이다. 본 모형에서는 유의확률이 0.01 이하로 유의미하다고 할 수 있다.
2. 두 번째 테이블은 모형에 의해 추정된 회귀계수 테이블이다. std err는 계수 추정치의 기본 표준오차, t는 t-value, P > | t |는 유의확률이다. 분석결과, 절편과 독립변수인 방문빈도는 모두 유의하다.
3. 세 번째 테이블에서는 잔차의 분포를 평가하기 위한 통계량이 나타난다. 산출 결과에 따르면, 잔차의 분포는 정규분포라고 보기 어렵다. (왜도, 첨도 및 독립성에 대한 용어는 생략, 마지막 condition number는 다중공선성을 평가할 수 있는 통계량으로, 일반적으로 30보다 작은 숫자가 나왔을 경우 다중공선성이 없다고 판단한다.)
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
matplotlib.rcParams['font.family'] = 'Malgun Gothic' # 한글 폰트 변경시 깨짐 방지
fit = np.polyfit(df['방문빈도'], df['총_매출액'], 1)
fit_fn = np.poly1d(fit)
print(np.round(fit, 3))
print(fit_fn)
%matplotlib inline
plt.title('단순회귀선')
plt.xlabel('방문빈도')
plt.ylabel('총매출액')
plt.plot(df['방문빈도'], df['총_매출액'], 'o')
plt.plot(df['방문빈도'], fit_fn(df['방문빈도']), 'r')
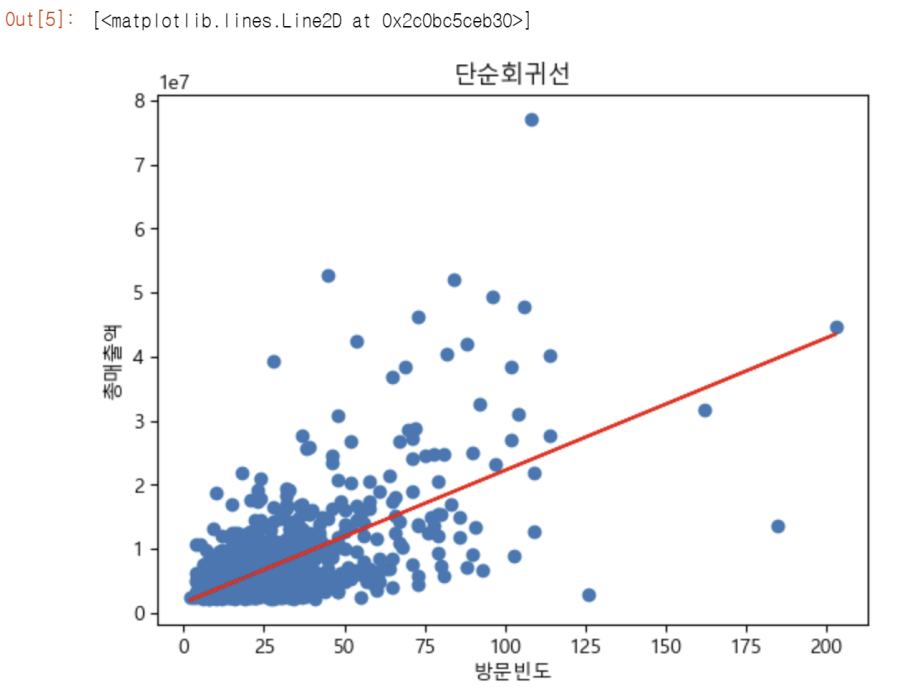
# 결론
도출된 회귀모형의 유의확률은 0.00이하로 통계적으로 유의하다. 회귀모형은 총 매출액의 39.8%를 설명한다고 볼 수 있다. 절편값은 1,572,000, 독립변수 x의 계수값은 206,600이므로 회귀식은 Y = 1,570,000 + 206,600 x 방문빈도가 된다. 즉, 방문빈도가 1회 높아질수록 총 매출액이 약 206,600원 증가하는 것을 의미한다. 따라서 A 쇼핑은 방문빈도 횟수를 높이는 방안으로 고려해야 하며, 매출액에 영향을 줄 수 있는 다른 요인도 찾는 방안을 모색해야 한다.
2) 다중회귀분석
단순회귀분석의 확장버전이라고 할 수 있다. 독립변수가 여러 개인 경우를 다루는 다중회귀분석은 실제 자료를 분석하는데 매우 유용하며 단순회귀분석에 비해 활용도가 매우 높다. 2개 이상의 독립변수(ex. 서비스 만족도, 방문횟수, 거래기간)가 1개의 수치형 종속변수(ex. 총 구매액)에 어떤 영향을 미치는지 등을 검정하는 통계분석기법이다.
i개의 독립변수 X1, ... Xi가 있는 다중회귀모형은 다음과 같다.
👉 Y = B0 + B1X1 + ...BiXi + Ei
단순회귀분석과 마찬가지로, 잔차제곱합을 최소화하는 최소제곱법에 의해 회귀모수를 추정할 수 있으며, 추정된 회귀계수를 b0, b1, ... bi라고 하면, 적합된 회귀식은 다음과 같이 주어진다.
👉 Y = b0 + b1X1 + b2X2 + ... biXi
단순회귀분석에서와 마찬가지로 다중회귀분석 결과의 해석에 있어서도 결정계수(R^2)는 회귀모형의 설명력을 나타내는 지표로 활용된다. 즉 결정계수 값이 1에 가까울수록 회귀모형의 설명력이 높다고 할 수 있다.
다만, 다중회귀모형에서는 독립변수가 추가됨에 따라 결정계수 값이 증가하기 때문에 결정계수 값이 높은 모형이 좋은 모형이라고 단정할 수는 없다. 불필요한 독립변수가 추가되어도 결정계수가 커지기 때문이다. 이 문제에 대한 방안으로 수정결정계수(혹은 조정결정계수)를 사용한다. 독립변수를 추가함에 따라 수정결정계수는 증가와 함께 다시 감소하기 때문에, 수정결정계수 값이 최대가 되도록 모형을 선택할 수 있다.
결국 최종적으로 위 가정들이 맞는지 확인하고, 적절치 않은 가정이 존재할 경우엔 모형수정을 통해 회귀모형을 재적합시켜야 한다!!
이미지 출처)
"https://www.flaticon.com/kr/free-icons/-" 아이콘 제작자: paonkz - Flaticon
'데이터 분석(DA) > 📊 통계분석' 카테고리의 다른 글
| 군집분석 (1) | 2024.02.26 |
|---|---|
| 분산분석 (2) | 2024.02.03 |
| 신뢰성 분석 (0) | 2024.01.23 |
| 범주형 데이터의 분석 (0) | 2024.01.12 |
| 상관관계 분석 (0) | 2024.01.06 |
