
주류를 효과적으로 구분하는 방법은 없을까?
알코올, 도수, 당도, pH값으로 와인의 종류를 구분해보자!
Chapter 05 - 1
# 로지스틱 회귀
1. 데이터 불러오기
> 와인 데이터를 우선 불러오자.
import pandas as pd
wine = pd.read_csv("https://bit.ly/wine-date")
wine.info() # info 메서드(데이터프레임의 각 열의 데이터 타입과 누적된 데이터가 있는지 확인한다.)
wine.describe()

평균, 표준편차, 최소, 1사분위수, 중간값/2사분위수, 3사분위수, 최대값이 나옴. 데이터의 수는 같으나, 그 단위(스케일)가 다름을 알 수 있다.
사이킷런의 StandardScaler 클래스로 특성을 표준화하자.
2. 세트 분류
data = wine[['alcohol', 'sugar', 'pH']].to_numpy() # wine 데이터프레임의 처음 3개 열을 넘파이 배열로 바꿔서 data배열에 저장했다.
target = wine['class'].to_numpy() # 마지막 class 배열도 넘파이 배열로 바꾸어 target배열에 저장했다.
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(data, target, test_size = 0.2, random_state = 42 )
print(train_input.shape, test_input.shape)
# (5197, 3) (1300, 3) > 훈련세트 5197개, 테스트 세트 1300개.
3. 전처리(스탠다드 스케일링)
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_scaled, train_target)
print(lr.score(train_scaled, train_target))
print(lr.score(test_scaled, test_target))
# 0.7808350971714451
# 0.7776923076923077 # 점수가 그닥 높진 않은 듯하다.
print(lr.coef_, lr.intercept_) # 로지스틱 회귀 모델의 계수와 절편을 출력했다.
# [[ 0.51270274 1.6733911 -0.68767781]] [1.81777902]> y = x1 * 0.51270274 + x2 * 1.6733911 + x3 * (-0.68767781) + 1.81777902
의 식을 도출할 수 있다. 알코올의 도수와 당도가 높을수록 화이트 와인일 가능성이 높고, pH가 높을수록 레드와인일 가능성이 높다. But, 정확히 이 숫자가 무엇을 의미하는지 로지스틱 모델은 설명하기 어렵다는 단점이 있다. 또, 다항 특성을 추가한다면, 설명하기가 더 난감할 것이다.
> 이를 해결할 수 있는 다른 모델은 없을까?
# 결정 트리
> 결정 트리는 다른 모델에 비해, '그 이유를 설명하기가 쉽다'는 장점이 있다. 데이터를 잘 나눌 수 있는 질문을 찾는다면, 계속 질문을 추가함으로써 분류 정확도를 높일 수 있다. 한번 결정 트리 모델을 통해 score를 확인해보자.
from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(random_state = 42)
dt.fit(train_scaled, train_target)
print(dt.score(train_scaled, train_target))
print(dt.score(test_scaled, test_target))
# 0.996921300750433
# 0.8592307692307692> 로지스틱 회귀 모델보다 점수가 훨씬 높지만, 다소 과대적합된 모습이다.
# 결정 트리 모형
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
plt.figure(figsize = (10, 7))
plot_tree(dt)
plt.show() # 결정 트리의 모형이 어떻게 형성되는지 확인하는 사이킷런의 plot_tree() 함수이다.
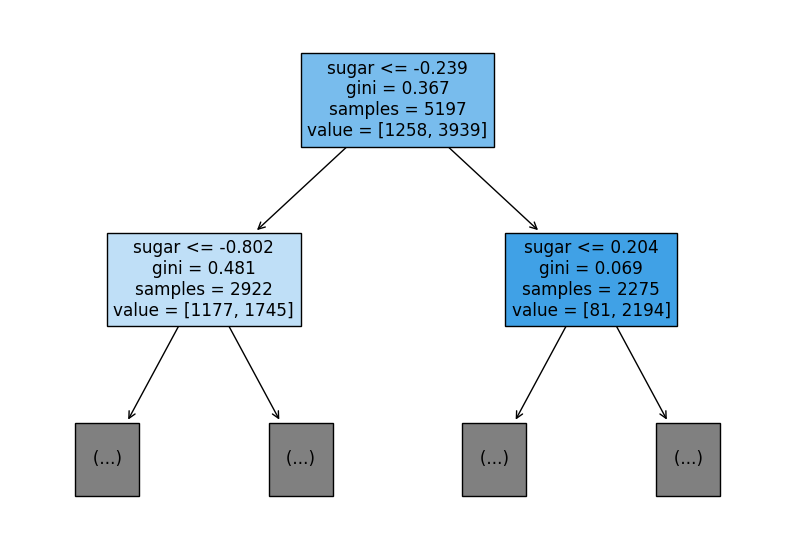
> 그림이 복잡하니, 트리의 깊이를 제한해보자.
plt.figure(figsize = (10, 7))
plot_tree(dt, max_depth = 1, filled = True, feature_names = ['alcohol', 'sugar', 'pH'])
plt.show()
# 테스트 조건(sugar)
-> 불순도(gini) -> 총 샘플 수(samples) -> 클래스별 샘플 수(value)
1. root 노드 (음성클래스 - 레드 와인 샘플 수: 1,258 개 / 양성클래스 - 화이트 와인 샘플 수: 3,939 개)
- 당도(sugar)가 -0.239 이하인가?
yes: 왼쪽 노드로 감 / no: 오른쪽 노드로 감.
2. 왼쪽 leaf 노드 (음성클래스: 1,177개 / 양성클래스: 1,745개)
- 당도가 -0.802보다 낮거나 같은가?
yes: 왼쪽 노드로 감 / no: 오른쪽 노드로 감.
3. 오른쪽 leaf 노드 (음성클래스: 81개 / 양성클래스: 1,745개)
- 당도가 0.204보다 낮거나 같은가?
> 각각의 노드 내부터 있는 음성/양성 클래스의 비율에 따라 색깔의 진함을 달리해주었음(filled = True). 그래서 오른쪽 노드의 색깔이 진하다고 볼 수 있음.
*** 결정 트리에서 예측하는 방법은 k-최근접 이웃과 비슷함. 각각의 리프 노드에서 가장 많은 클래스가 예측 클래스가 됨.
# 불순도(gini)
> 지니 불순도(gini impurity). 결정트리classifier 클래스의 'criterion 매개변수'의 기본값이 바로 'gini'다. 노드에서 데이터를 분할할 기준을 정하는 것이 바로 이 criterion 매개변수의 용도다. 지니 불순도는 클래스의 비율을 제곱하여 더한 다음 1에서 빼면 된다.
지니 불순도 = gini > gini = 1 - ( 음성클래스 비율 ^ 2 + 양성클래스 비율 ^ 2)
예시)
root 노드: 1 - ((1258/5197) ^ 2 + (3939/5192) ^ 2) = 0.367
leaf 노드: 1 - ((1177/2922) ^ 2 + (1745/2922) ^ 2) = 0.481> 결정 트리 모델은 부모 노드(parent node)와 자식 노드(child node) 간의 불순도 차이가 가능한 크도록 트리를 성장시킨다. 불순도 차이를 계산하는 방법은 다음과 같다.
부모의 불순도 - (왼쪽 노드 샘플 수 / 부모의 샘플 수) * 왼쪽 노드 불순도 - (오른쪽 노드 샘플 수 / 부모의 샘플 수) * 오른쪽 노드 불순도
정보이득(information gain) = 0.367 (2922/5197) * 0.481 - (2275/5197) * 0.069 = 0.066> 이 알고리즘은 정보 이득이 최대가 되도록 데이터를 나눈다!
+ criterion = 'entropy'를 지정하여 엔트로피 불순도를 사용할 수도 있다. 지니 불순도와는 다르게 제곱이 아닌, 밑이 2인 로그를 사용해 곱한다. 보통 엔트로피 불순도와 지니 불순도 간 결과의 차이는 크지 않다. 결국, 불순도 기준을 사용해 정보 이득이 최대가 되도록 노드를 분할하는 것이 중요한 것!
# 가지치기
1. 최대 깊이 지정하기
dt = DecisionTreeClassifier(max_depth = 3, random_state = 42)
dt.fit(train_scaled, train_target)
print(dt.score(train_scaled, train_target))
print(dt.score(test_scaled, test_target))
# 0.8454877814123533
# 0.8415384615384616
2. 트리 모형 확인하기
plt.figure(figsize = (10, 7))
plot_tree(dt, filled = True, feature_names = ['alcohol', 'sugar', 'pH'])
plt.show()
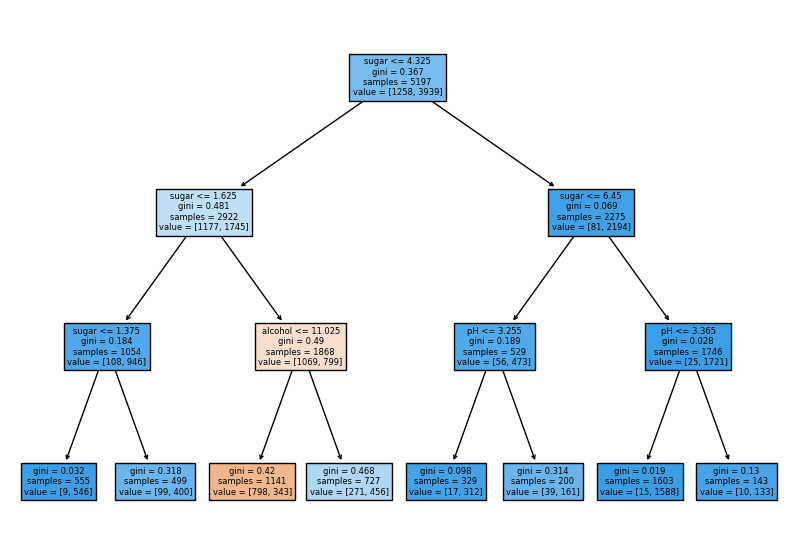
> 깊이 1의 노드(인덱스랑 같은 개념)는 모두 당도(sugar)를 기준으로 훈련 세트를 나눔. 깊이 2의 노드는 알코올 도수(alcohol)와 pH를 기준으로 나눔. 깊이 3에 있는 노드가 최종 리프 노드인데, 왼쪽에서 세 번째 있는 노드만 음성클래스의 비율이 더 높은 것을 알 수 있다. 이 노드에 도착해야만 레드 와인으로 예측할 것이다. 그리고 당도는 - 0.239 보다 작고, -0.802보다 작아야 하며, 알코올 도수는 0.454보다 작거나 같아야 한다.
### But, 뭔가 이상하지 않은가? 당도와 도수가 어떻게 음수(-)가 나오지?
불순도는 각 클래스의 비율을 가지고 계산했다. 그리고 앞서 불순도를 기준으로 샘플을 나눈다고 했다.
그렇다면, 샘플을 어떤 클래스 비율로 나눌 지 계산할 때, 특성값의 스케일이 계산에 영향을 미치지
않음을 알 수 있다! 따라서 결정 트리 방식을 사용할 때 우리는 데이터 특성값의 스케일링, 즉 전처리
스케일링을 굳이 할 필요가 없다. 다시 스케일링 하기 이전의 샘플로 결정 트리 모델을 돌려보자.# 데이터 scaling을 하지 않은 기존 input 데이터
dt = DecisionTreeClassifier(max_depth = 3, random_state = 42)
dt.fit(train_input, train_target)
print(dt.score(train_input, train_target))
print(dt.score(test_input, test_target))
# 0.8454877814123533
# 0.8415384615384616plt.figure(figsize = (10, 7))
plot_tree(dt, filled = True, feature_names = ['alcohol', 'sugar', 'pH'])
plt.show()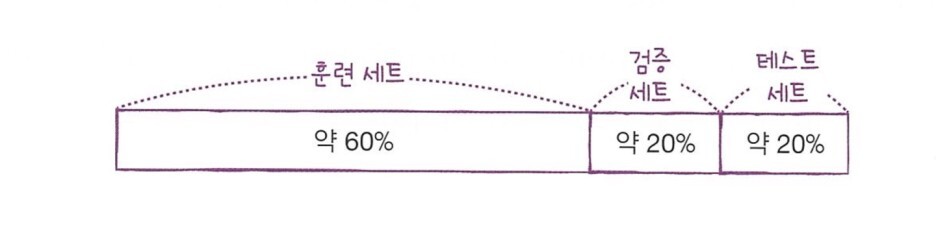
# 특성 중요도 확인하기
print(dt.feature_importances_)
# [0.12345626 0.86862934 0.0079144 ]> 두 번째 특성인 '당도'의 특성 중요도가 가장 높다. 특성 중요도는 각 노드의 정보 이득과 전체 샘플에 대한 비율을 곱한 후 특성별로 더하여 계산한다. 특성 중요도를 활용하면 결정 트리 모델을 특성 선택에 활용할 수 있다는 장점이 있다!
Chapter 05 - 2. 교차 검증
> 테스트 세트의 과도한 사용은 테스트 세트에 적합한 모델을 만들기 쉽다. 훈련 세트를 통해 모델의 훈련이 충분히 이뤄지고 난 뒤, 테스트 세트는 최종적으로 검증하는데 쓰는 것이 가장 바람직하기에, 우리는 아래와 같이 훈련 세트를 다시 한 번 나눠볼 것이다. 훈련 세트와 검증 세트로 말이다.
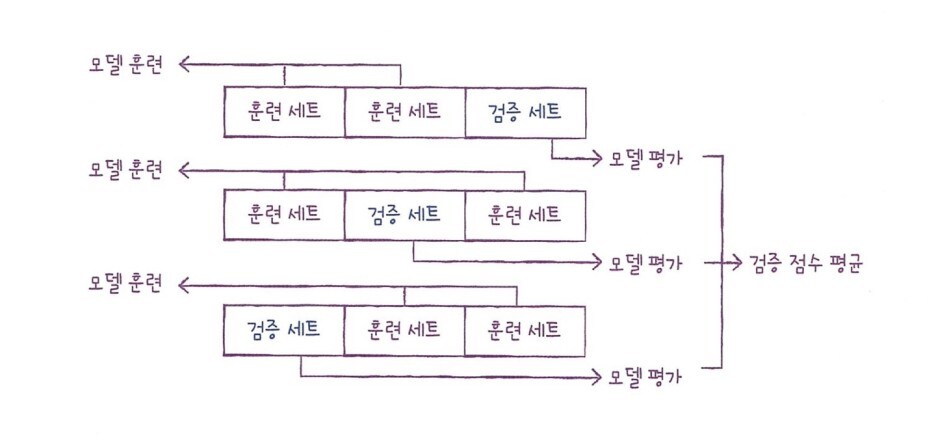
### train_input과 train_target 을 각각 sub와 val에 나누어 저장한다.
sub_input, val_input, sub_target, val_target = train_test_split(train_input, train_target, test_size = 0.2, random_state = 42)
print(sub_input.shape)
print(val_input.shape)
# (4157, 3)
# (1040, 3)from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(random_state = 42)
dt.fit(sub_input, sub_target)
print(dt.score(sub_input, sub_target))
print(dt.score(val_input, val_target))
# 0.9971133028626413
# 0.864423076923077> 잘 나뉘어져서 훈련된 것을 확인했다! 다소 과대적합되었지만, 매개변수를 적절하게 수정하면 된다.
여기서 잠깐!
> 우리는 검증 세트를 만들기 위해 훈련 세트의 0.2 정도를 떼었다. 보통 많은 데이터를 훈련에 사용할수록 좋은 모델이 만들어지기 때문에, 검증 세트를 교차로 사용해 그것의 평균을 구하면, 기존의 훈련 데이터를 잃지 않고 효과적으로 검증 과정을 거칠 수 있다.
> 3 - 폴드 교차 검증이란, 훈련 세트를 3부분으로 나누어 검증을 하는 것을 말하는데, 보통 5, 10 - 폴드 교차 검증을 많이 사용한다.
+ 사이킷런에는 cross_validate()라는 교차 검증 함수가 있다. 책의 내용을 참고해 코드를 작성해보자.
from sklearn.model_selection import cross_validate
scores = cross_validate(dt, train_input, train_target)
print(scores)
# {'fit_time': array([0.06197739, 0.0489049 , 0.02641892, 0.06654239, 0.05361962]),
# 'score_time': array([0.01214767, 0.00172496, 0.02446532, 0.00183868, 0.00163984]),
# 'test_score': array([0.86923077, 0.84615385, 0.87680462, 0.84889317, 0.83541867])}> fit_time : 모델을 훈련하는 시간, score_time : 검증하는 시간, test_score : 검증 폴드의 점수
print(np.mean(scores['test_score']))
# 0.855300214703487> 검증 폴드의 평균 점수(최상의 검증 점수)를 가늠해볼 수 있다. 여기서 주의할 점은 cross_validate()는 훈련 세트를 섞어 폴드를 나누지 않는다는 점이다. 우리는 앞서 train_test_split을 통해 전체 데이터를 섞은 후 훈련 세트를 준비했기 때문에 따로 섞을 필요가 없지만, 교차 검증을 할 때 훈련 세트를 섞으려면 분할기(spliter)를 지정해야 한다. 여기서는 목적이 분류 모델이므로, StratifiedKFold 를 사용할 것이다.
# 하이퍼 파라미터 튜닝
> 모델이 학습할 수 없어 사용자가 지정해야 하는 매개변수다. 사이킷런과 같은 머신러닝 라이브러리를 사용할 때 이런 하이퍼 파라미터는 모두 클래스나 매서드의 매개변수로 표현된다. 먼저 라이브러리가 제공하는 기본값을 그대로 사용해 모델을 훈련하는데, 검증 세트의 점수나 교차 검증을 통해 매개변수를 조금씩 바꿔나간다. 하지만, 각 매서드마다, 각 클래스마다 매개변수의 개수도 다르고, 또 하나만 바꾼다고 되는 것이 아니다. 때문에, 우리는 for문을 구현해 최적의 파라미터를 구할 수도 있겠지만, 그보단 사이킷런에서 제공하는 그리드 서치를 사용할 것이다.
from sklearn.model_selection import GridSearchCV # 그리드 서치CV 클래스를 임포트하고 탐색할 매개변수와 탐색할
# 값의 리스트를 딕셔너리로 만든다.
params = {'min_impurity_decrease': [0.0001, 0.0002, 0.0003, 0.0004, 0.0005]}
gs = GridSearchCV(DecisionTreeClassifier(random_state = 42), params, n_jobs = -1) # cv 매개변수 기본값은 5, min_impurity_decrease 값마다 5-폴드 # 교차 검증을 수행한다. 결국 5 * 5 = 25개의 모델을 훈련한다.
gs.fit(train_input, train_target)> 교차 검증에서 최적의 하이퍼파라미터를 찾으면 전체 훈련세트로 모델을 다시 만들어야 했다. 하지만 그리드 서치에서는 훈련이 끝나면 25개의 모델 중에서 검증 점수가 가장 높은 모델의 매개변수 조합으로 전체 훈련세트에서 자동으로 다시 모델을 훈련한다. 이 모델은 gs 객체의 best_estimator_ 속성에 저장되어 있고, 이 모델을 결정 트리 모델처럼 똑같이 사용 가능하다.
dt = gs.best_estimator_
print(dt.score(train_input, train_target))
# 0.9615162593804117
print(gs.best_params_) # 최적의 매개변수 찾기
# {'min_impurity_decrease': 0.0001}
print(gs.cv_results_['mean_test_score']) # 교차 검증의 평균 점수 추출하기
# [0.86819297 0.86453617 0.86492226 0.86780891 0.86761605]
best_index = np.argmax(gs.cv_results_['mean_test_score'])
print(gs.cv_results_['params'][best_index])
# {'min_impurity_decrease': 0.0001}> 1. 탐색할 매개변수를 찾는다.2. 훈련 세트에서 그리드 서치를 수행해 최상의 평균 검증 점수가 나오는 매개변수 조합을 찾느다. 이 조합은 그리드 서치 객체에 저장된다. 그리드 서치는 최상의 매개변수에서 전체 훈련 세트를 사용해 최종 모델을 훈련한다. 이 모델도 그리드 서치 객체에 저장된다.
# min_impurity_decrease
> 노드를 분할하기 위한 불순도 감소 최소량을 지정하는 것.
+ max_depth로 트리의 깊이를 제한한다.
+ min_samples_split으로 노드를 나누기 위한 최소 샘플 수도 골라본다.
params = {'min_impurity_decrease': np.arange(0.0001, 0.001, 0.0001),
'max_depth' : range(5, 20, 1),
'min_samples_split' : range(2, 200, 10)
}
gs = GridSearchCV(DecisionTreeClassifier(random_state = 42), params, n_jobs = -1) # 총 9 * 15 * 10 = 1350 번의 교차검증 횟수가 수행됨.
gs.fit(train_input, train_target)
print(gs.best_params_)
# {'max_depth': 14, 'min_impurity_decrease': 0.0004, 'min_samples_split': 12}
print(np.max(gs.cv_results_['mean_test_score']))
# 0.8683865773302731> 그리드서치 클래스를 활용하니 매개변수를 일일이 변경하면서 교차 검증을 수행하지 않고도 원하는 매개변수 값을 나열하며 자동으로 교차 검증을 수행했고, 결국 최상의 매개변수를 찾을 수 있었다. 그렇다면, 우리는 매개변수의 간격을 꼭 위에서처럼 0.0001, 1로 설정하지 않아도 되는 것일까?
# 랜덤 서치
> 매개변수의 값이 수치일 때, 값의 범위나 간격을 미리 정하기 어려울 수 있다. 또 너무 많은 매개변수 조건이 있어 서치 수행 시간이 오래 걸리기도 한다.(이게 가장 큰 단점인 듯.) 이럴 때 우린 랜덤 서치를 사용할 수 있다.
그리드 서치와는 다르게, params의 값의 목록을 전달하지 않고, 랜덤 서치는 매개변수를 샘플링할 수 있는 확률 분포 객체를 전달한다. 싸이파이에서 2개의 확률 분포 클래스를 임포트해보겠다.
from scipy.stats import uniform, randint
rgen = randint(0, 10)
rgen.rvs(10)
# array([8, 7, 0, 4, 2, 5, 6, 0, 5, 2])
np.unique(rgen.rvs(1000), return_counts = True)
# (array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),
# array([104, 102, 98, 101, 96, 100, 97, 98, 96, 108]))
ugen = uniform(0, 1)
ugen.rvs(10)
# array([0.25733225, 0.00267421, 0.93724408, 0.85478063, 0.43766382
# , 0.58204653, 0.17552338, 0.15198423, 0.54608093, 0.65156915])> stats 서브 패키지에 있는 uniform과 randint 클래스는 모두 주어진 범위에서 고르게 값을 뽑는다. 이를 '균등 분포에서 샘플링한다.'고 말하는데, randint는 정수값을 뽑고, uniform은 실수값을 뽑는다. 난수 발생기랑 유사하다. 랜덤 서치에 randint와 uniform 클래스의 객체를 넘겨주고, 몇 번을 샘플링해서 최적의 매개변수를 찾으라고 명령할 것이다. 탐색할 매개변수는 다음과 같다.
params = {'min_impurity_decrease': uniform(0.0001, 0.001),
'max_depth' : randint(20, 50),'min_samples_split' : randint(2, 25),'min_samples_leaf' : randint(1, 25)
}
from sklearn.model_selection import RandomizedSearchCV
gs = RandomizedSearchCV(DecisionTreeClassifier(random_state = 42), params,
n_iter = 100, n_jobs = -1, random_state = 42)
gs.fit(train_input, train_target)
print(gs.best_params_)
# {'max_depth': 39, 'min_impurity_decrease': 0.00034102546602601173, 'min_samples_leaf': 7, 'min_samples_split': 13}
print(np.max(gs.cv_results_['mean_test_score']))
# 0.8695428296438884> 이제 이 모델을 최종 모델로 설정하고, test 세트로 성능을 확인해보자.
dt = gs.best_estimator_
print(dt.score(test_input, test_target))
# 0.86> 우리는 레드와인과 화이트 와인을 선별하기 위해 결정 트리의 다양한 하이퍼파라미터를 시도해보았다. 이 과정에서 테스트 세트를 계속해서 사용하다 보면, 결국 훈련 세트가 아닌 테스트 세트에 적합한 모델을 만들게 된다.
테스트 세트는 최종 검증과 모델의 선택 때까지 사용해선 안된다. 때문에, 모델의 훈련 적합도를 판단하기 위해 훈련 세트를 다시 검증세트와 훈련세트로 분류하는 작업을 거쳤다. 검증 세트를 통해 모델이 잘 학습되었는지 판단을 하는데, 어떻게 데이터를 나누었냐에 따라 검증 점수가 들쭉날쭉할 수 있어 다시 검증하는 프로세스를 여러 번 거쳤다. 이를 우리는 교차 검증이라고 한다.
> 그리고 이 교차 검증을 시도함에 있어, 다양한 하이퍼 파라미터를 탐색하게 되는데, 머신러닝 라이브러리에서는 각종 클래스와 메서드의 매개변수를 바꾸어 모델을 훈련하고 평가한다. 이 과정을 단순화하고 좀 더 빠르게 할 수 있도록 도와주는 것이 바로 그리드 서치와 랜덤 서치이다.
Chapter 05 - 3. 트리의 앙상블
# 정형 데이터 / 비정형 데이터
> 사실 데이터의 종류에 관해서는 다들 익히 들어 알고있을 것이다. 앞 장에서 생선의 길이, 높이, 무게, 두께 등을 데이터로 사용했다. csv파일에 저장되어 있는 형태였는데, 이렇게 구조화된 종류의 데이터가 바로 '정형 데이터'이다. 반면, 데이터베이스나 엑셀로 표현하기 어려운 데이터(ex. 글, 텍스트, 사진, 음악 등)는 '비정형 데이터'라고 한다.
> 여기서 정형 데이터를 가장 잘 다룬다고 알려진 알고리즘이 바로 '앙상블 학습'이다. 이 앙상블 학습의 대표적인 모델이 바로 '랜덤 포레스트'이다. 이름에서 유추가 가능하듯이, 랜덤 포레스트는 결정 트리를 랜덤하게 만들어, 결정 트리의 숲을 이룬다. 여기서, 각 트리의 예측을 사용해 랜덤 포레스트의 최종 예측을 내놓는데, 이 성능이 가히 정형 데이터를 다루는데 있어 정점이라고 할 수 있다.
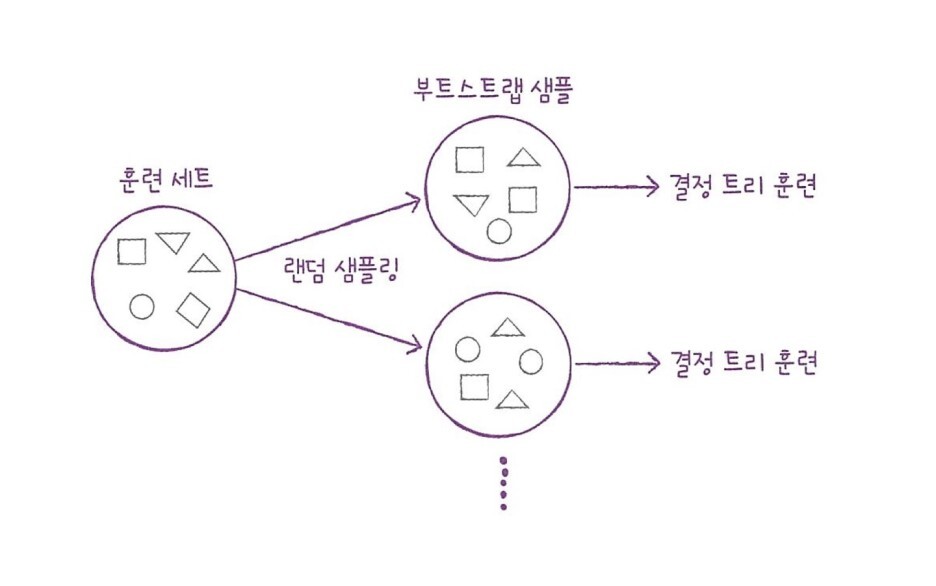
> 먼저, 랜덤 포레스트는 각 트리를 훈련하기 위한 데이터를 랜덤하게 만든다. 우리가 입력한 데이터들 가운데, 샘플들을 랜덤하게 추출하여 훈련 데이터를 만든다. 여기서 주목할 점은, 한 샘플이 중복되어 추출될 수 있다는 점이다. 예를 들어 1000개의 가방에서 100개씩 샘플을 뽑는다면, 먼저 1개를 뽑고, 뽑은 1개를 다시 가방에 넣는다. 이런 식으로 반복해서 100개를 가방에서 뽑으면, 중복된 샘플을 뽑을 수 있다. 이렇게 만들어진 샘플을 '부트스트랩 샘플'이라고 한다. 그리고 기본적으로 부트스트랩 샘플의 크기는 훈련세트의 크기와 동일하다. 다만, 중복된 값이 있냐 없냐의 차이일 뿐이다.

> 또한, 각 노드를 분할할 때, 전체 특성 중에서 일부 특성을 무작위로 고른 다음 이 중에서 최선의 분할을 찾는다. 분류 모델인 RandomForestClassifier는 전체 특성 개수의 제곱근만큼의 특성을 선택한다. -> 4개의 특성이 있다면 2개의 특성을 랜덤하게 선택하여 사용함. 분류일 때는 각 트리의 클래스별 확률을 평균해서 가장 높은 확률을 가진 클래스를 예측으로 삼는다. 그리고, 랜덤하게 샘플과 특성을 사용하기 때문에, 훈련 세트에 과대적합되는 것을 막아주고 검증 세트와 테스트 세트에서 안정적인 성능을 얻을 수 있다. 그럼 랜덤포레스트 모델을 사용한 와인 분류를 해보자.
from sklearn.model_selection import cross_validate
from sklearn.ensemble import RandomForestClassifier # 랜덤 포레스트는 결정 트리의 앙상블. 때문에 결정트리classifier가 제공하는 # 매개변수는 모두 제공한다.
rf = RandomForestClassifier(n_jobs = -1, random_state = 42)
scores = cross_validate(rf, train_input, train_target,
return_train_score = True, n_jobs = -1)
print(np.mean(scores['train_score']), np.mean(scores['test_score']))
# 0.9973541965122431 0.8905151032797809> 훈련 세트에 다소 과대적합된 모습이다. 결정 트리의 장점 중 하나인 특성 중요도를 계산함에 있어, 랜덤 포레스트의 특성 중요도는 각 결정 트리의 특성 중요도를 취합한 것과 같다.
rf.fit(train_input, train_target)
print(rf.feature_importances_)
# [0.23167441 0.50039841 0.26792718]> 랜덤 포레스트는 특성의 일부를 랜덤하게 선택해 결정 트리를 훈련하기 때문에, 어떤 특성 하나에 치우치지 않고 좀 더 다양한 특성이 훈련에 참여할 수 있도록 도와준다. 이는 훈련 세트에 과대적합되는 것을 줄이고 일반화 성능을 높이는데도 도움을 준다.
> 앞서 부트스트랩 샘플을 사용하게 되면, 중복된 샘플이 훈련 데이터에 저장된다고 했다. 그렇다면, 중복되거나 훈련데이터에도 포함되지 않는 잉여 데이터는 어떻게 되는가? 랜덤 포레스트는 이 남은 샘플을 일컬어 OOB(out of bag) 샘플이라고 하는데, 이 남은 샘플을 사용해 부트스트랩 샘플로 훈련한 결정 트리를 평가할 수 있다. 잉여 데이터가 곧 검증 세트로 탈바꿈한다고 볼 수 있다.
rf = RandomForestClassifier(oob_score = True, n_jobs = -1, random_state = 42)
rf.fit(train_input, train_target)
print(rf.oob_score_)
# 0.8934000384837406> 교차 검증에서 얻은 테스트 세트의 score와 비슷한 결과를 얻었다. 이처럼 OOB는 교차 검증을 대신할 수 있어 결과적으로 더 많은 훈련 데이터를 사용할 수 있다는 장점이 있다.
# 엑스트라 트리
> 기본적으로 랜덤 포레스트와 비슷하게 작동한다. 100개의 결정 트리를 훈련하고, 결정트리가 제공하는 대부분의 매개변수를 제공한다. 그리고 전체 특성 중에서 일부 특성을 랜덤하게 선택해 노드를 분할하는데 사용한다.
> 랜덤 포레스트와 엑스트라 트리의 차이점은 부트스트랩 샘플을 사용하지 않는다는 점이다. 결정 트리를 만들 때, 전체 훈련 세트를 사용한다. 대신, 노드를 분할할 때, 최선의 분할 즉 가장 좋은 분할을 찾지 않고, 무작위로 분할한다. 성능은 낮아질 수 있지만, 그만큼 많은 트리를 앙상블하기 때문에, 과대적합을 막고, 검증 세트의 점수를 높이는 효과가 있다.
from sklearn.ensemble import ExtraTreesClassifier
et = ExtraTreesClassifier(n_jobs = -1, random_state = 42)
scores = cross_validate(et, train_input, train_target,
return_train_score = True, n_jobs = -1)
print(np.mean(scores['train_score']), np.mean(scores['test_score']))
# 0.9974503966084433 0.8887848893166506> 특성이 많지 않는 모델이기 때문에, 랜덤 포레스트와 비슷한 결과를 얻었다. 엑스트라 트리가 무작위성이 좀 더 크기 때문에, 랜덤 포레스트보다 더 많은 결정 트리를 훈련해야 한다. 하지만, 랜덤하게 노드를 분할하기 때문에, 랜덤 포레스트보다는 계산 속도가 더 빠르다.
# 그레디언트 부스팅(gradient boosting)
> 깊이가 얕은 결정 트리를 사용해 이전 트리의 오차를 보완하는 방식으로 앙상블을 한다. 사이킷런의 GradientBoostingClassifier는 기본적으로 깊이가 3인 결정 트리를 100개 사용하는데, 깊이가 얕은 결정 트리를 사용하기 때문에 과대적합에 강하고 높은 일반화 성능을 기대할 수 있다. 여기서는 4장에서 다루었던 경사하강법을 사용해 트리를 앙상블에 추가한다. 분류에서는 로지스틱 손실함수를 사용하고, 회귀에서는 평균 제곱 오차 함수를 사용한다.
from sklearn.ensemble import GradientBoostingClassifier
gb = GradientBoostingClassifier(random_state = 42)
scores = cross_validate(gb, train_input, train_target,
return_train_score = True, n_jobs = -1)
print(np.mean(scores['train_score']), np.mean(scores['test_score']))
# 0.8881086892152563 0.8720430147331015> 깊이가 낮은 트리를 사용하는 만큼, 과대적합에 강한 양상이 확연히 드러난다.
gb = GradientBoostingClassifier(n_estimators = 500, learning_rate = 0.2,
random_state = 42)
scores = cross_validate(gb, train_input, train_target,
return_train_score = True, n_jobs = -1)
print(np.mean(scores['train_score']), np.mean(scores['test_score']))
# 0.9464595437171814 0.8780082549788999> n_estimator(결정 트리의 개수)의 default값이 100인 반면에 5배나 늘린 500개로 했음에도 과대적합을 잘 억제하는 모습이다.
gb.fit(train_input, train_target)
print(gb.feature_importances_)
# [0.15872278 0.68010884 0.16116839] # 그레디언트 부스팅도 특성 중요도를 제공한다.> 일반적으로 그레디언트 부스팅이 랜덤 포레스트보다 조금 더 높은 성능을 얻을 수 있다. 하지만, 그만큼 순서대로 트리를 추가하기 때문에 훈련의 속도가 느리다. 이 속도의 문제점을 개선한 것이 바로 히스토그램 기반 그레디언트 부스팅이다.
# 히스토그램 기반 그레디언트 부스팅
> 정형 데이터를 다루는 머신러닝 알고리즘 가운데 인기가 가장 높은 알고리즘. 가장 먼저 입력 특성을 256개의 구간으로 나누는데, 이는 노드를 분할할 때 최적의 분할을 빠르게 찾을 수 있게 도와준다.(??? 이 말이 잘 이해가 되지 않는다...) 따라서 입력에 누락된 특성이 있더라도 따로 전처리할 필요가 없다고 한다.
from sklearn.experimental import enable_hist_gradient_boosting
from sklearn.ensemble import HistGradientBoostingClassifier
hgb = HistGradientBoostingClassifier(random_state = 42)
scores = cross_validate(hgb, train_input, train_target,
return_train_score = True)
print(np.mean(scores['train_score']), np.mean(scores['test_score']))
# 0.9321723946453317 0.8801241948619236> 특성 중요도를 살펴보자.
hgb.fit(train_input, train_target)
print(rf.feature_importances_)
# [0.23167441 0.50039841 0.26792718]
> 테스트 세트의 최종 score도 확인해보겠다.
hgb.score(test_input, test_target)
# 0.8723076923076923> 우리는 사이킷런 이외의 라이브러리도 살펴볼 필요가 있다. 대표적인 히스토그램 기반 그레디언트 부스팅 알고리즘은 사이킷런의 패키지에서 사용되지만, XGBoost와 마이크로소프트에서 만든 LightGBM도 있다. (있다는 사실만 알아두자..! 나중에 필요하면 쓰겠지..)
# keyword
- 결정 트리(의사 결정 트리)
- 앙상블 학습
- 랜덤포레스트
- 교차검증
- 그레디언트 부스팅
- 정형 데이터
이미지 출처)
"https://www.flaticon.com/kr/free-icons/" 아이콘 제작자: Nuricon - Flaticon
'머신러닝(ML), 딥러닝(DL)' 카테고리의 다른 글
| 인공신경망(ANN)과 활성화 함수 [딥러닝] (0) | 2024.03.13 |
|---|---|
| 퍼셉트론(Perceptron) [딥러닝] (0) | 2024.03.12 |
| 비지도 학습 [머신러닝] (1) | 2024.01.13 |
| 회귀 알고리즘과 모델 규제 [머신러닝] (0) | 2023.12.21 |
| 로지스틱 회귀(Logistic Regression) [머신러닝] (0) | 2023.12.15 |
