기술통계분석

jo._.on_ 2023. 12. 31. 16:01

아래 글은 모두 'step by step [파이썬 비즈니스 통계분석]' 교재를 기초로 진행한 내용입니다. 모든 장은 이전 장과 이어져 있으니, 세부 내용 및 이전 글이 궁금하시다면 해당 블로그의 이전 장과 교재를 참고해주시면 되겠습니다.~~

기초통계량

1. 평균

'평균'은 데이터의 중심 성향을, '분산'과 '표준편차'는 데이터의 퍼짐 정도를 나타낼 수 있는 대표적인 기초통계량이다. 자료들의 중심 성향 특징을 나타내는 대표값. 사용 목적에 따라 크게 산술평균, 기하평균, 조화평균으로 구분 가능하다.

1) 산술평균 : 자료들의 전체 합을 자료의 개수로 나눈 값. (우리가 흔히 평균을 계산한다~라고 했을 때 생각하는 값)
2) 기하평균 : 자료들의 곱을 자료 수만큼 제곱근한 값.

Ex) 예금 이자의 복리계산 같은 곱셈으로 계산하는 값들의 평균을 계산하고자 할 때 주로 사용된다. n개의 양수가 있을 때, 이들 수의 곱의 n제곱근 값이 기하평균값. 일반적으로 기하평균은 산술평균보다 크지 않다.

3) 조화평균 : n개의 양수에 대해 그 역수들을 산술평균하고, 이를 다시 역수로 취한 값.

Ex)

주로 데이터의 평균적인 변화율이나 업무능률의 평균을 구하고자 할 때 주로 사용된다.

>> 기하평균과 조화평균은 특수한 경우에만 거의 사용되고, 특별한 설정이 없을 경우 통계분석 소프트웨어는 대부분 산술평균을 의미한다.

2. 분산과 표준편차

자료의 퍼짐 정도를 나타내는 통계량. 산술평균(평균)이 갖지 못하는 자료의 산포도를 제공하는 지표이다.

ex) A 쇼핑은 고객에게 쿠폰으로 증정된 할인권의 사용 횟수에 대해 평균과 분산 및 표준편차를 성별에 따라 구하려 한다. 할인권의 사용 횟수 평균과 분산에 따라 고객에게 제공하는 쿠폰제공 횟수를 조절할 수 있고, 성별에 따라 할인권 사용 횟수에 대한 분포가 다르다면 성별에 따른 차별화된 할인쿠폰 제공 전략을 시행할 수 있다.

# 실습

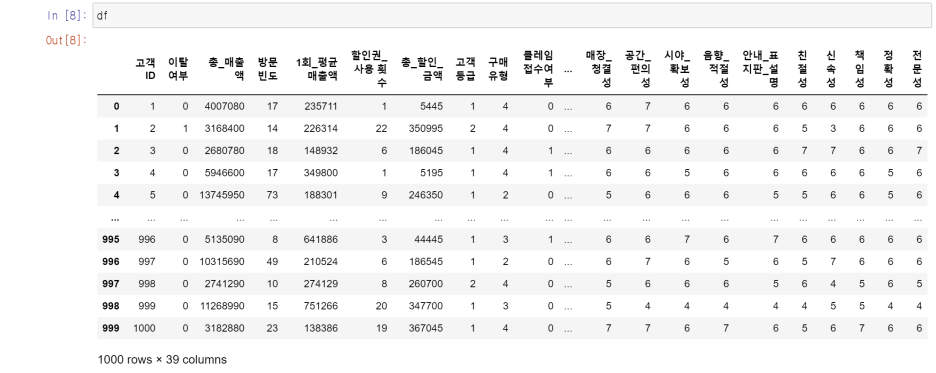
1. df의 데이터프레임 형태를 확인하기.

import numpy as np # numpy 라이브러리.
import pandas as pd # pandas 라이브러리.
import matplotlib.pyplot as plt # 추후 왜도, 첨도 구할 때 사용할 라이브러리.

df = pd.read_csv(".../Ashopping.csv", encoding = 'CP949')
df

2. df의 할인권 사용 횟수와 성별 특성을 df_1에 새로 할당했다. 성별 특성에 따라 groupby를 해주고, 남녀의 할인권 사용 횟수의 '평균', '분산', '표준편차'를 출력했다.

df_1 = df[['할인권_사용 횟수', '성별']]

print(df_1.groupby('성별').mean()) # 평균
print(df_1.groupby('성별').var()) # 분산
print(df_1.groupby('성별').std()) # 표준편차

> 할인권 사용횟수의 평균은 약 16회, 표준편차는 약 8.3회 정도.

1년에 30회의 할인쿠폰을 제공하는 A 쇼핑몰 입장에서는 할인쿠폰 전략이 우수한 성과를 보인다고 할 수 있다. 따라서, 성별에 따른 개별적인 할인쿠폰 제공 전략을 모색하지 않아도 된다.

3. 왜도와 첨도

분산과 표준편차로 자료의 퍼짐, 산포도를 파악할 수 있지만, 해당 산포도의 구체적인 특성까지 판단할 수는 없다. 왜도와 첨도는 산포도의 치우침과 뾰족함을 나타냄으로써 산포도의 외형적인 특징을 보다 잘 설명할 수 있도록 해준다.

1) 왜도(Skewness): 자료들의 분포가 왼쪽 또는 오른쪽으로 치우쳐 있는 정도를 나타내는 통계량.

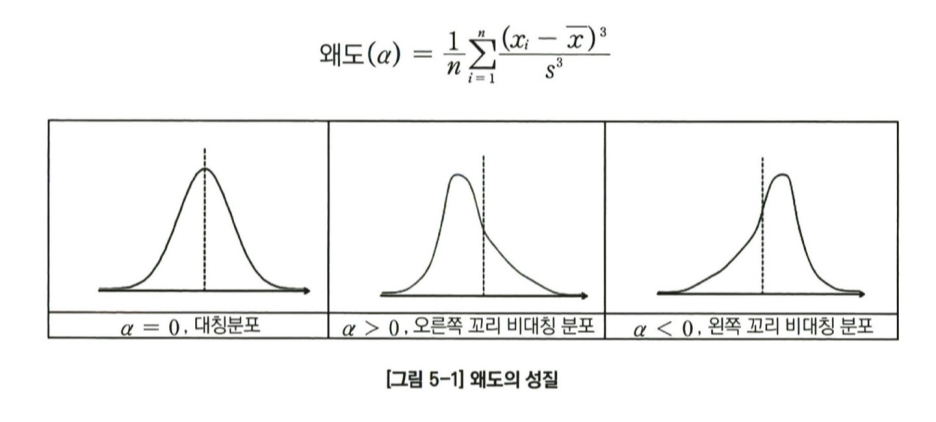
왜도 값이 0보다 큰 값을 가질 경우에는 전체적인 분포가 왼쪽으로 치우쳐진 오른쪽 꼬리 비대칭 분포를 보인다. 반대로, 왜도 값이 0보다 작을 경우에는 전체 분포가 오른쪽으로 치우쳐진 왼쪽 꼬리 비대칭 분포를 띈다. But, 왜도값이 0일 때는 대칭 분포를 보인다!

2) 첨도(Kurtosis): 분포의 뾰족한 정도를 나타내는 값, 자료들이 얼마나 평균에 집중되어 있는지 확인할 수 있는 통계량.

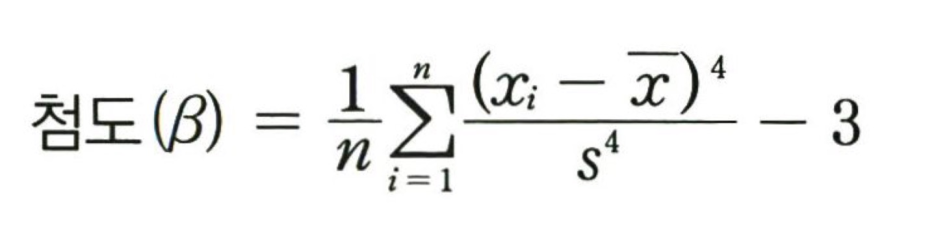
0을 기준으로 0보다 크면, 정규분포보다 뾰족한 분포의 형태를 보인다. 반대로 0보다 작으면, 정규분포보다 완만한 구릉 모양으로 분포를 띈다.

# 실습

>> 이론적인 특징만으로는 명확하게 받아들이기가 어렵다. 어따 써먹는지 실습을 통해 한 번 알아보자.

Ex) A 쇼핑몰의 서비스 만족도에 대한 왜도와 첨도.

print(df['서비스 만족도'].skew())
print(df['서비스 만족도'].kurt())

%matplotlib inline
df.서비스 만족도.hist(bins = 7)

# -0.9706614...
# 1.14782458...

> 전체적으로 값이 오른쪽으로 치우쳐진 왼쪽 꼬리 비대칭 분포와, 첨도값이 1.14 정도로 정규분포보다 뾰족한 형태를 띄고 있다.

따라서 A 쇼핑몰의 고객서비스 만족도는 평균값인 5.54에 비해 다소 높게 평가하는 고객들이 많음을 알 수 있다.

기타 기술통계량

평균, 분산, 표준편차, 왜도, 첨도 외에도 데이터의 특성을 나타내는 기술통계량은 다양하게 존재한다.

Ex)

중앙값, 최빈값: 산술평균과 마찬가지로 데이터의 대표성을 나타내는 지표.
사분위수: 왜도와 첨도처럼 전체 데이터의 분포적 특성을설명하는 보조적 지표.

1. 중앙값(median)

'자료를 크기 순서대로 늘어놓았을 때, 가장 중앙에 위치한 값.

가장 직관적이면서도 간단한 지표다. (단, 자료의 개수에 따라 구하는 방식이 다르니, 아래 예시를 보고 참고할 것.)

Ex) 자료의 수가 홀수일 경우 중앙값은 자료의 수+1을 2을 나눈 값의 순번에 위치한 값이 중앙값이 된다.

{1, 3 ,5} 의 중앙값: 자료의 수 = 3, 여기에 +1 한 뒤, 2로 나눈 순번의 값 = 3이 중앙값.

Ex) 자료의 수가 짝수일 경우 자료의 수를 2로 나눈 값의 순번에 위치한 값과 자료의 수 + 2를 2로 나눈 값의 순번에 위치한 값의 산술평균값이 중앙값이 된다.

{1, 4, 6, 9} 의 중앙값: 자료의 수 = 4(4 / 2 = 2), + 2 하면 6(6 / 2 = 3) -> 두 개를 각각 2로 나눈 뒤, 해당 순번의 값(4, 6)의 평균{(4 + 6)/ 2}을 구한다. (4 + 6) / 2 = 5가 중앙값

2. 최빈값(mode)

자료에서 가장 많이 관측되는 수치를 의미한다. 중앙값과 마찬가지로 자료의 대표성을 나타내는 보조적 지표. 단, 최빈값은 하나의 값만을 가지지 않는다. 두 개일 경우의 분포를 이봉분포, 세 개 이상의 경우를 다봉분포라고 한다. 그리고, 모든 자료의 값의 수가 동일할 경우에는 최빈값이 존재하지 않는다!

Ex)

{1, 2, 3, 4, 5, 6} -> 최빈값 x. {1, 1, 1, 3, 4, 5} -> 최빈값: 1

3. 사분위수(quartile)

자료들을 크기 순서대로 늘어놓았을 때 누적 백분율을 4등분한 각 점에 위치한 값.

1사분위수 = 전체 누적백분율 중 25%에 위치한 값.
2사분위수 = 전체 누적백분율 중 50%에 위치한 값.
3사분위수 = 75%.
4사분위수 = 100%.

# 실습

>> 얜 또 어디에 써먹는데??
ex) 예금 이자의 복리계산 같은 곱셈으로 계산하는 값들의 평균을 계산하고자 할 때 주로 사용.

n개의 양수가 있을 때, 이들 수의 곱의 n제곱근 값이 기하평균값. 일반적으로 기하평균은 산술평균보다 크지 않다.

Ex) A 쇼핑몰의 정기적 할인쿠폰 발송에 대한 예시다.

고객 별로 매월 1~2 장 정도 발송하는데, 고객들의 평균적인 할인쿠폰 사용빈도는 연 16회이므로, 현 발송 횟수가 적절하다고 생각해왔다. But 할인쿠폰 사용빈도의 평균만으로는 의사결정의 신뢰성이 떨어질 수 있기 때문에, 중앙값, 최빈값 같은 기술 통계량으로 다시 타당성을 검증해볼 필요가 있다.

1. 각 할인권 사용 횟수의 사분위수와 최빈값, 기타 기술통계량 출력하기.

# 백분위수를 출력하는 percentile 함수.
# 25, 50, 75, 100으로 사분위수를 구분한 뒤 출력한다.
print(np.percentile(df['할인권_사용 횟수'], 25))
print(np.percentile(df['할인권_사용 횟수'], 50))
print(np.percentile(df['할인권_사용 횟수'], 75))
print(np.percentile(df['할인권_사용 횟수'], 100))

# 그리고, 가장 많은 수의 자료를 idxmax함수를 사용해 최빈값으로 출력한다.
print('최빈값: ', df['할인권_사용 횟수'].value_counts().idmax())

# describe() 함수로 각각의 기술통계량을 다 출력한다.
print('기술통계량: '\n', df['할인권_사용 횟수'].describe())

최빈값 22회 : 연간 22회 정도를 사용하는 고객이 가장 많다!
할인권 사용의 중간수준인 2사분위는 연간 17회 정도를 사용.

> 상위 고객으로 갈수록 연간 할인권 사용 횟수가 많아짐을 알 수 있다. 즉, 소비를 많이 하는 고객일수록 연간 할인권을 많이 사용한다고 볼 수 있다.